GaAsのヘテロ構造に閉じ込められた2次元電子系などでは、電子系のウィグナー結晶と量子液体の間の量子相転移が観測される。このような電子ガスは電子間の平均距離(r_s)によって量子効果の大きさを測ることができる。ところがこの電子ガスとしてみた場合の電子間距離が小さく、普通ならば量子融解して液体となっているはずの高い電子濃度でも電子の結晶化が見られることがある。ペロブスカイト酸化物、有機化合物などに広範に見られる電荷秩序やストライプと呼ばれるものがそれである。この電荷秩序は大概電子濃度が、固体の原子の結晶の周期との間に簡単な関係(整合性)を満たすときだけに見られる。例えば原子の結晶の数単位格子あたり電子が1つ(すなわち単位格子あたりの電子濃度(フィリングと呼ばれる)が1/2や1/3のような簡単な分数)の時にのみ結晶化し、そこからずれた電子濃度のときは、電子濃度がピン止めされたり、融けて金属となる。これは電子濃度の外部周期ポテンシャルに対するコメンシュラビリティ(整合性)が高いときにウムクラップ散乱の効果によって、絶縁体化したものと考えられるが、はっきりしたことは知られていなかった。平均場計算をすると整合性の有無にそれほど依らずに、ゆらぎの無視のために結晶化してしまうことも理解を遅らせていた。
我々の経路積分繰り込み群の計算によって、電子濃度が簡単な分数で表される整合性の高い濃度になるほど顕著に結晶化しやすくなることがはっきり示された。(フィリングが1/2にもなると、結晶化する電子濃度は連続空間で整合効果のない電子ガスに比べて、1/100程度にまで小さくなる)。この結果、普段単純に金属と分類しているような、電子がバンドの途中までしか埋まっていない系でも、電子相関の強い場合には、有理分数フィリングによる電荷秩序の可能性がいたるところにある。「バンド理論による金属と絶縁体」という単純な分類とは違う複雑な構造が形成されることがわかった。この結果はなぜ単純なフィリングのときにだけ電荷秩序が実験的に見出されやすいのかをよく説明する。
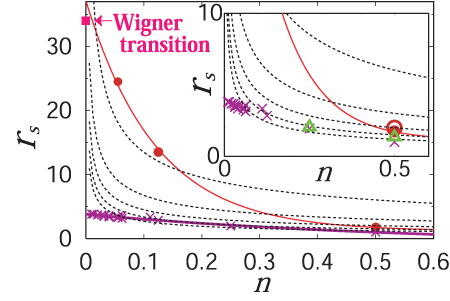
図1:電子のフィリングがn=1/k(kは整数)のような分数フィリングのときの結晶相と量子液体相の相図。赤い曲線が相図の境界。縦軸r_sは電子のボーア半径でスケールした電子間平均距離。1つの物質で電子のフィリングを変えると大雑把には黒点線の曲線上を動き、kの減少とともに電荷秩序相の領域が拡大する。簡単な分数のフィリングでのみ、ウムクラップ絶縁体(電荷秩序)が安定化されるという実験事実がよく理解できる。ハートレーフォック近似の相境界は紫色の曲線であり、この場合電荷秩序の安定化の様相が正しく理解できない。(挿入図はr_sが小さいところの拡大図)
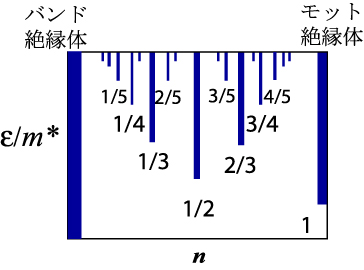
図2:バンド絶縁体(左端)とハーフフィリングで生ずるモット絶縁体(右端)の間で、バンド理論では普通の金属と考えられる領域にも、誘電率εと電子の有効質量m*の比(縦軸)の大きさに応じて、さまざまな周期の電荷秩序が生じる様子をあらわす概念図。フィリングが簡単な分数の時に電荷秩序の安定化される領域(図の青く塗られた領域)が大きい。
「研究の概要」へ戻る