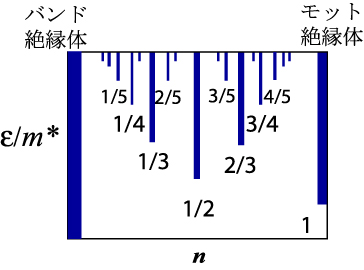
量子系の数値シミュレーションは電子相関やその他の多体相関の大きな量子系の物理を解明する上で重要である。シミュレーションのアルゴリズムは1970年代以降、活発に研究が行なわれ、以下に述べるようにいくつものアルゴリズムが開発された。しかしどのアルゴリズムにも、それぞれに長所と欠点がある。数値計算を行なう場合には解明すべき問題に応じて、適したアルゴリズムを使い分けなければならない。特に強相関電子系のシミュレーションは最も難しいことが知られている。今まで知られている理論模型の計算アルゴリズムには、ハミルトニアン行列の厳密な対角化、種々の量子モンテカルロ法があり、また一次元的な形状の格子に対しては、転送行列法や密度行列繰り込み群が知られている。厳密な対角化で扱える理論模型の系のサイズは20サイト程度までで、それ以上は今後の計算機の性能の向上があっても困難である。また量子モンテカルロ法はより大きなサイズの計算が可能だが、しばしば負符号問題という困難が生じて、意味のある結果を得られないことがある。密度行列繰り込み群は2次元以上の系の計算には使えない。強相関電子系の研究では、20サイト程度までの理論模型のハミルトニアン行列の厳密な対角化の結果のみを用いたものが大変多い。しかし大きなサイズ(熱力学極限)への外挿を行なうことなく、小さなクラスターの定性的なふるまいだけから、相転移周辺の性質を議論することは大変無茶なことである。
経路積分繰り込み群法は上記の種々の困難を克服する方法として、2年程前に本研究室で開発された。本研究室では現在も絶えずその改良を通じて、新たな問題へ応用した研究を続けている。またこの手法は、物性物理学の多電子系の問題だけでなく、原子核の殻模型の計算にも用いられるようになってきている。
経路積分繰り込み群法のアルゴリズムでは、経路積分を用いながら、繰り込み群的にヒルベルト空間の拡大(射影)と選択(切断)を効率良く進める。この結果、与えられたヒルベルト空間の次元の範囲内で基底状態や低エネルギー励起状態の最良の変分波動関数をバイアスなしに数値的に生成する。さらにヒルベルト空間の次元を系統的に拡大して外挿を行なう。経路積分作用素から数値的に生成される非直交基底の選択を最適化することで高い精度が得られる。非直交基底選択の数値的最適化は配置相互作用(CI)法やランチョス法などと比較して大変速い収束を示し、大きな系の扱いが可能となる。我々はこのアルゴリズムの有効性を詳細に検討し、ハバード模型の16サイトまでの厳密対角化計算との比較、100サイト程度で量子モンテカルロ計算が行える場合との比較を通じて、高い精度と適用領域の広さを検証した。この結果は量子モンテカルロ法の負符号問題などのために今まで困難が大きくてどの手法でも扱えなかった問題に取り組むことができることを示している。(M. Imada and T. Kashima: J. Phys.Soc. Jpn. 69(2000) 2723および T. Kashima and M. Imada: J. Phys.Soc. Jpn. 70(2001) 2287)
またこの手法では出発点で何らかの一体近似(ハートレーフォック近似など)が再現され、系統的にゆらぎが取り込まれるため、解析や評価、他の手法の結果との比較を行ないやすいという特徴がある。収束を早めるために、ヒルベルト空間の拡大と射影というプロセスとともに、電子相関効果をグッツウィラー因子やジャストロ因子のような相関因子を含めて取り込んでおくというアルゴリズムの改良も進めている。この段階でこの手法は変分モンテカルロ法を第ゼロ近似とする系統的改良としての性格も兼ね備えることとなる。この手法はどのような格子の形状の問題にも使えるし、負符号問題の困難もない。
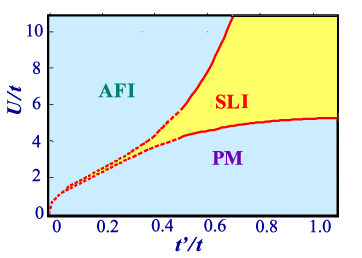
この新しいアルゴリズムを応用した最初の研究は、幾何学的なフラストレーションのある格子フェルミオン系の性質の解明についてである。具体的には、次近接トランスファーt’のために幾何学的フラストレーションの効果の顕著な2次元ハバード模型を研究し、金属絶縁体転移と反強磁性転移の存在とその性格を明らかにして、t'と相互作用Uの大きさのパラメータ空間での相図を求めた。特に反強磁性絶縁体相と常磁性金属相に挟まれて、非磁性絶縁体相が広く存在するという、下図、図1のような今まで予想されなかった結果を得た(T. Kashima and M. Imada: J. Phys.Soc. Jpn. 70(2001)3052; H. Morita, S. Watanabe and M. Imada: cond-mat/0203020)。2次元以上の系で、並進対称性の破れを伴わない量子スピン液体の可能性とそのスピン液体に隣接する金属相の可能性は、アンダーソンの提唱に始まり、大変多く議論されてきた。例えば、最近は弱結合の繰り込み群によって、反強磁性の対称性の破れを伴わない「ウムクラップ絶縁体」の存在の可能性が議論された。この相図で得られている非磁性絶縁体相は有限の大きさのU/tの時に、対称性の破れを伴わずにウムクラップ散乱によって駆動される非磁性絶縁相が存在することを示した最初のはっきりした例である。またモット絶縁体と金属の間の転移にはフィリング制御型とバンド幅制御型の2つの重要なタイプがあることが知られていたが、この研究では今まで困難の大きかったバンド幅制御型の金属絶縁体転移をはじめて数値的に解明することに成功した。非磁性絶縁相が相図の中に広い領域を占めていることから、この相の存在を実験的に検証するのは大変興味深い問題である。実際にこの研究で調べられた非等方的な三角格子模型は有機導体であるBEDT-TTF化合物のための単純化された理論模型として知られていた。ごく最近、斎藤、鹿野田らのグループはBEDT-TTF化合物に属し、アニオンがCu_2(CN)_3である物質をしらべ、ESR(電子スピン共鳴)だけでなく、NMR(核磁気共鳴)の実験結果でも1.4Kの低温まで磁気秩序の見られない絶縁体であることを発見した。本研究室で得られた非磁性絶縁相との関連が興味ある課題となっている。

一方、本研究室では、連続空間で長距離クーロン相互作用があるときの経路積分繰り込み群アルゴリズムの開発も進めた。長距離クーロン相互作用があるときの格子上のハバード模型は連続極限で連続空間の電子ガスの系につながる。この研究で電子間のクーロン相互作用によって、多電子系は量子液体と固体との間の相転移を起こす。この融解、固化に際して、原子による周期ポテンシャルがあると、電子の固体相(ウィグナー結晶、電荷秩序、モット絶縁体など)の安定性が、電子密度と原子の結晶格子定数との整合性によって決定的な影響を受けることを見出した。簡単な整合性があるときにのみ電子の電荷秩序が見出されるという普遍的な現象の理解が定量的に可能になるとともに、バンドが埋まっていない金属相の持つ複雑な構造が明らかとなった。